Flow Through A Rectangular Slot
Orifice Discharge into Free Air
- Viscous Flow Through Rectangular Slot
- Flow Through A Rectangular Slotted
- Air Flow Through Rectangular Slot
- Flow Through A Rectangular Sloth
An orifice is an opening with a closed perimeter through which water flows. Orifices may have any shape, although they are usually round, square, or rectangular.
Discharge through a sharp-edged orifice may be calculated from:

Flow Rate Calculator. Easily calculate the volumetric flow rate of a pipe (a.k.a. Discharge rate) given its diameter (for a round pipe, height & width for a rectangular one) and the velocity of the liquid or gas flowing through it. The flow rate calculator can also calculate the mass flow rate of liquids given the liquid density is known. Flow through a rectangular weir can be expressed in imperial units with the Francis formula. Q = 3.33 (b - 0.2 h) h 3/2 (1b) where. Q = flow rate (ft 3 /s) h = head on the weir (ft) b = width of the weir (ft) Alternative with height in inches and flow in gpm: Triangular or V-Notch Weir.

Q = Ca?2gh
where
Q= discharge, ft3/s (m3/s)
C =coefficient of discharge
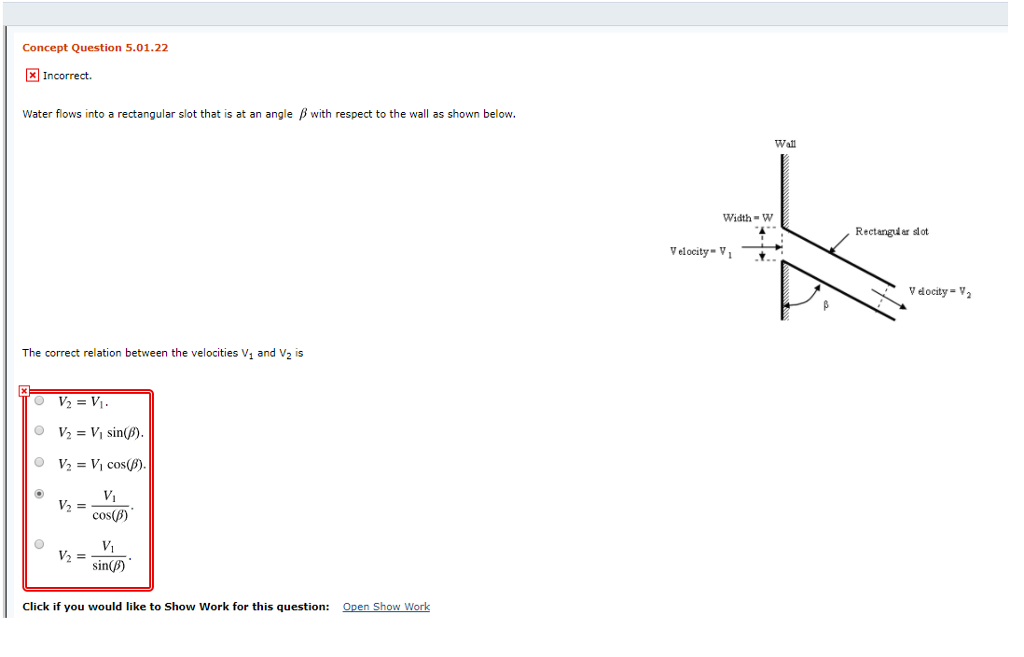
Viscous Flow Through Rectangular Slot
a =area of orifice, ft2 (m2)
g =acceleration due to gravity, ft/s2 (m/s2)

h =head on horizontal center line of orifice, ft (m)
The coefficient of discharge C is the product of the coef- ficient of velocity Cv and the coefficient of contraction Cc. The coefficient of velocity is the ratio obtained by dividing the actual velocity at the vena contracta (contraction of the jet discharged) by the theoretical velocity. The theoretical velocity may be calculated by writing Bernoulli’s equation for points 1 and 2.Thus
V2= ?2gh
Flow Through A Rectangular Slotted
The coefficient of contraction Cc is the ratio of the smallest area of the jet, the vena contracta, to the area of the orifice.
Air Flow Through Rectangular Slot
Submerged Orifices
Flow Through A Rectangular Sloth
Flow through a submerged orifice may be computed by applying Bernoulli’s equation to points 1 and 2 in figure below
Values of C for submerged orifices do not differ greatly from those for nonsubmerged orifices.